The realm of quantum computing holds the potential to revolutionize various fields by solving problems deemed intractable for classical computers. However, achieving this potential necessitates precise quantum simulations that can accurately mimic complex quantum systems. Researchers from notable institutions, including Freie Universität Berlin and Google AI, have recognized the need to adeptly estimate Hamiltonian parameters for bosonic excitations within superconducting quantum simulators. Their recent work, shared in a preprint on arXiv, marks a significant advancement that could set the stage for higher accuracies in quantum simulations and understanding complex systems.
The genesis of this research stemmed from a phone call that Jens Eisert, the lead author, received while attending a conference. His connections within the Google AI team expressed their struggles with calibrating the Sycamore superconducting quantum chip. This collaborative effort came at a crucial moment, as the team was grappling with the complexities of Hamiltonian learning, facing significant setbacks. Initially, Eisert presumed that resolving their issues would be straightforward; however, as he delved deeper, he discovered that misestimations in the Hamiltonian operator frequencies rendered the task far more complex than anticipated.
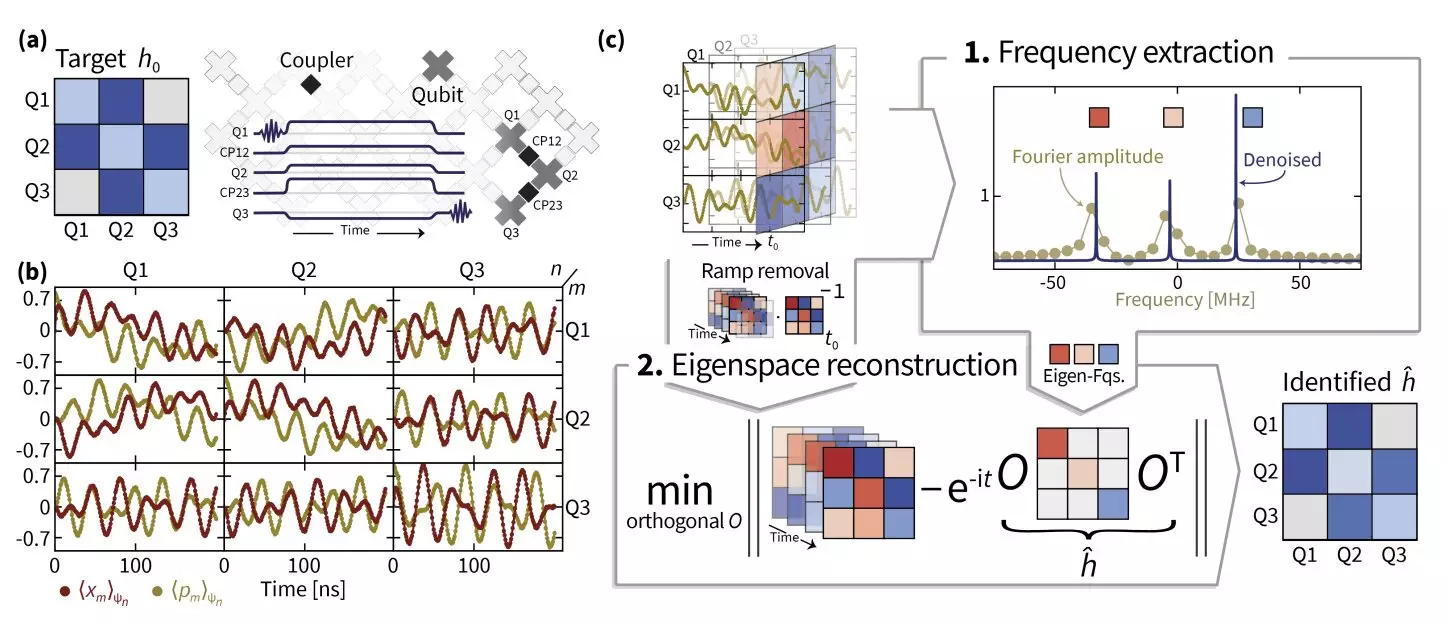
Understanding the intricacies behind the Hamiltonian dynamics called for a multi-faceted approach. Eisert enlisted the expertise of Ph.D. students Ingo Roth and Dominik Hangleiter, leading them to explore superresolution methodologies. The process was exploratory, revealing not only the technical complications laid bare by actual data but also the collaborative dynamics necessary for innovation. The research team’s persistence ultimately bore fruit through a blend of theoretical advancements and practical experimentation, demonstrating the delicate balance that defines successful scientific inquiry.
The project’s innovative backbone consisted of superresolution techniques aimed at refining eigenvalue estimations. Moreover, the application of manifold optimization was pivotal in accurately restoring the eigenspaces of the Hamiltonian operator. This technique stands out because it enables researchers to handle variables residing in smooth, complex spaces instead of traditional Euclidean frameworks. Eisert noted that attention to the functionality of the system activation processes was vital, as real-world fluctuations can cause deviations from ideal Hamiltonian behavior, complicating data fitting.
The researchers introduced TensorEsprit, a novel technique for implementing superresolution which synergized with manifold optimization to yield robust estimates of Hamiltonian parameters. Their framework enabled them to identify Hamiltonian parameters for up to 14 coupled superconducting qubits, which is a remarkable achievement considering the historical challenges associated with Hamiltonian learning in practical circumstances.
The culmination of their research provided insightful revelations into why publications on Hamiltonian learning are scarce. The difficulty in obtaining reliable data and results in practical experiments has frequently deterred advancements in this area. As Eisert and his team engaged with data derived from tangible experiments, they realized the sheer complexity involved in characterizing Hamiltonians experimentally.
Their findings suggest that with the right methodology, scaling these techniques up for large quantum processors may be feasible. The implications of this research are profound: if validated, these approaches could pave the way for further advancements in understanding and manipulating quantum systems.
Looking ahead, Eisert’s team aims to extend the application of their methods to various interacting quantum systems. Inspired by their success, they are exploring tensor network theories in conjunction with cold atomic systems—an area pioneered by physicist Immanuel Bloch. The fundamental question still remains: what exactly defines a Hamiltonian of a system? This simple query belies the complexity that underpins quantum mechanics where accuracy is paramount.
In quantum mechanics, data-driven insights hold less predictive power without a precise understanding of the Hamiltonian. The researchers’ future exploration into characterizing Hamiltonians through practical data could reshape our grasp of quantum technologies and broaden the horizons for analog quantum simulation.
The work accomplished by this collaborative team not only stands as a significant breakthrough in the field of quantum mechanics but also ushers in a new wave of inquiry into the nature of Hamiltonians themselves. By merging theoretical advancements with practical applications, they set a promising example for future research directions in the exploration of quantum systems, ultimately aiming for the realization of high-precision quantum simulations that could expand the capabilities of quantum technology. Through their efforts, the field of quantum computing may inch closer to its long-held promise of solving complex, real-world problems.

Leave a Reply